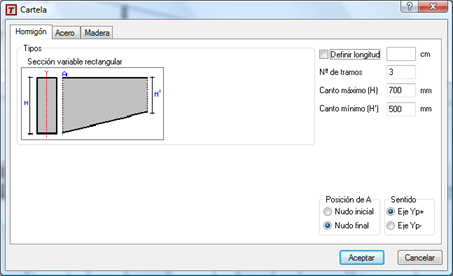
Muchas son las prestaciones que actualmente tienen los programas de cálculo de estructuras de hormigón, pero ninguno de ellos dispone de funciones para el cálculo y dimensionamiento de vigas de hormigón de inercia o canto variable. Arktec incorporará en la próxima versión de Tricalc la posibilidad de definir, calcular y obtención de planos de armaduras de este tipo de secciones.

La posibilidad de calcular una estructura como la de la imagen adjunta será una realidad en Tricalc 7.3:

Las vigas de inercia variable permiten optimizar el diseño de estructuras con grandes luces o cargas, añadiendo más canto sólo en las zonas donde realmente son necesarias.

La próxima versión del programa Tricalc permitirá la introducción de este tipo de vigas (o diagonales) de hormigón, siempre de sección rectangular. Aunque normalmente el aumento de canto se produce por la parte inferior de la viga, también será posible definir aumentos de canto por la parte superior (útil en cubiertas, por ejemplo). Con este mecanismo también es posible definir las típicas vigas ‘delta’ de las naves industriales prefabricadas de hormigón armado, aunque, de momento, deberán ser de sección rectangular y no pretensadas.

La introducción de estas vigas de inercia variable en hormigón será muy similar a la introducción de cartelas en madera o acero ya disponibles en versiones anteriores. Además, será posible definir en forjados reticulares y de losa maciza zunchos de sección asignada con inercia variable.

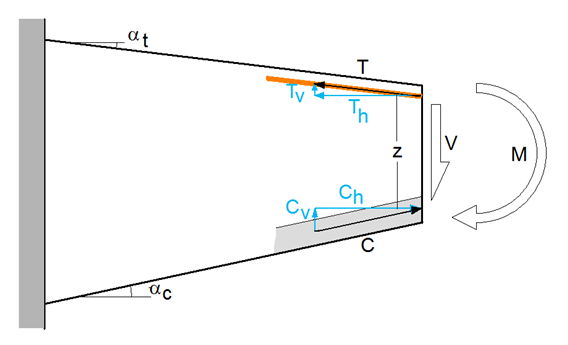
Cálculo del armado

La existencia de una inercia variable implica modificaciones tanto en el cálculo del armado longitudinal como del armado transversal de la pieza.

Para el armado longitudinal, hay que tener en cuenta que la armadura longitudinal que forme un ángulo a con la directriz de la viga, si el cálculo demanda un área necesaria (de tracción o de compresión) igual a As, deberá disponerse un área algo mayor igual a As / cos a .

Para la comprobación a cortante (y por tanto, para el cálculo de la armadura transversal), la existencia de armadura longitudinal y/o bielas de hormigón comprimido que formen un ángulo con la directriz de la pieza, puede ser beneficiosa o perjudicial, dependiendo del signo del momento flector y del signo del cortante. Por ejemplo, en un voladizo en el que el canto de la sección es mayor en su origen, tendremos (para más generalidad hemos utilizado una nomenclatura independiente de cualquier normativa):

Se cumple que

• Th = T•cos at

• Tv = T•sen at

• Ch = C•cos ac

• Cv = C•sen ac

• Th•z = Ch•z = M

Siendo

• V es el cortante actuante en la sección

• M es el momento actuante en la sección

• C es la compresión del hormigón respuesta de la sección

• T es la tracción de la armadura respuesta de la sección

• ac es el ángulo que forma la cara comprimida de la viga respecto a su directriz

• at es el ángulo que forma la cara traccionada de la viga (y por tanto la armadura de tracción) respecto a su directriz

• z es el brazo de palanca

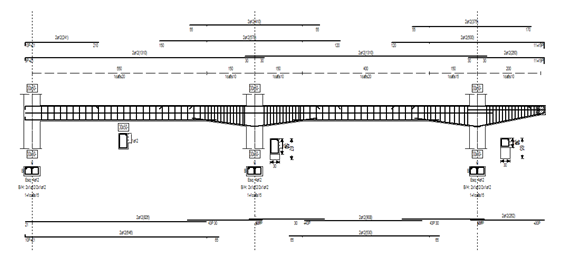
Se tiene entonces un cortante reducido (como definía la vetusta EH-91) ó efectivo (como define la actual EHE-08) de valor

Vr = V – Cv – Tv

con el que hay que realizar el dimensionado a cortante (nota: en la EN 1992-1-1, algunas comprobaciones se deben seguir realizando con el cortante inicial V). En este caso, Vr < V, pero, si por ejemplo la imagen correspondiera al arranque de una viga biapoyada (en la que el momento tiene sentido contrario al del dibujo), se tendría que Vr > V. Como regla práctica, el cortante efectivo será menor cuando la sección crece en la dirección en la que también crece el momento flector (en valor absoluto).

Planos de armado

Los nuevos planos de armado de Tricalc 7.3 recogerán toda la descripción de este tipo de elementos de inercia variable. La armadura que forma un ángulo con la directriz de la viga se dibujará en proyección, aunque acotando la longitud real de cada tramo, lo que aporta una gran claridad a los planos, manteniendo el estándar de versiones anteriores.