
Tricalc
Nuevas posibilidades de cálculo en 2º orden
Con la presentación de Tricalc 7.0 en 2008, incluyendo el cálculo de la estructura en 2º orden, se ha puesto a disposición de los usuarios nuevas posibilidades de cálculo, tanto en el tema del cálculo de la estructura deformada, como en el de los tirantes, apoyos unidireccionales y resortes trabajando sólo a compresión. La generalidad del método empleado hace que pueda ser aplicable a distintas situaciones de forma fácil y automática, sin más que activar la opción. Como ejemplo introductorio, si una estructura con cargas gravitatorias y de viento se calcula en 1º orden sólo una vez, con 26 hipótesis de carga para la obtención de sus desplazamientos, ahora con Tricalc es posible realizar en 2º orden tantos cálculos como combinaciones finales, en la práctica miles de procesos de resolución del sistema de ecuaciones, uno para cada combinación. Todo ello es posible gracias al nuevo motor de cálculo de resolución de ecuaciones implementado en Tricalc 7.0, con una velocidad de cálculo que permite resolver el sistema de ecuaciones en segundos.
Este artículo aborda los fundamentos del cálculo en 2º orden utilizado en Tricalc, su comparación con el cálculo en 1º orden y los beneficios de su aplicación en diferentes situaciones del cálculo de estructuras.
Diferencias entre cálculo en 1er orden y cálculo en 2º orden
Recordar en primer lugar, que para calcular los desplazamientos y giros de todos los nudos de una estructura debe resolverse el siguiente sistema de ecuaciones:
[K]·{d} = {F}
En el que [K] es la matriz de rigidez de la estructura, {d} son los desplazamientos y giros que se desean obtener, y {F} son las acciones exteriores -las cargas- aplicadas a la estructura.
La principal diferencia entre un cálculo elástico lineal en 1º orden y todos los tipos de cálculo en 2º orden es, que en el primer caso, se cumple el principio de superposición y en el segundo no. Es decir, en 1º orden es posible realizar el cálculo por separado para cada hipótesis simple de carga y posteriormente combinarlas para obtener las diferentes combinaciones de estado límite último y estado límite de servicio. Incluso es posible modificar los coeficientes parciales de seguridad de las acciones y obtener directamente las combinaciones sin volver a resolver el sistema de ecuaciones. Por tanto, en este caso, las matrices {d} y {F} poseen tantas columnas como hipótesis simples se desea considerar.
Sin embargo, para cualquier tipo de cálculo en 2º orden, al no cumplirse el principio de superposición, debe resolverse el sistema de ecuaciones para cada combinación de acciones a estudiar. Ello es debido a que [K] y/o {F} varían en función de {d}, lo que implica calcular por iteraciones o aproximaciones sucesivas, en las que tras cada iteración, se obtienen los desplazamientos y giros {d} a partir de los cuales se recalcula [K] y/o {F} para realizar la siguiente iteración, tal como se explica al hablar de los diferentes tipos de cálculo en 2º orden. Por tanto, en este caso, las matrices {d} y {F} poseen tantas columnas como combinaciones de acciones se desea considerar, y debe realizarse un cálculo por iteraciones, independiente para cada combinación.
Tipos de cálculo en 2º orden
Los diferentes tipos de cálculo en 2º orden, se agrupan en las siguientes categorías:
Cálculo en 2º orden geométrico o elástico: En este caso, se considera la posición de las cargas exteriores con respecto a la estructura deformada. Es decir, si por ejemplo, tras un primer cálculo en 1º orden un pilar de altura h que tiene una carga vertical P en su cabeza sufre un desplazamiento horizontal relativo de la cabeza de magnitud D1, aparece un momento de 2º orden de valor P·D 1, de ahí que este método se conoce como el método P-Delta (P·D). Este momento adicional (que puede definirse con un par de fuerzas horizontales de 2º orden en ambos extremos del pilar de valor H1 = P·D1 / h) produce, en un segundo cálculo (o iteración) un desplazamiento horizontal adicional D 2 (que en general será menor que D 1), y así sucesivamente, hasta que en la iteración n, el desplazamiento adicional D n se considere suficientemente pequeño, y menos a un valor definible.
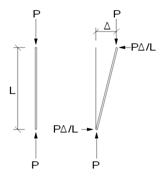
Método de 2º orden P·D , utilizado por Tricalc 7
Cálculo en 2º orden mecánico o plástico. En este caso, se tienen en cuenta las no linealidades del material. En el caso de estructuras metálicas, el caso típico corresponde a la formación de rótulas plásticas (generalmente en las uniones entre elementos), en las que existe una gráfica momento – giro no lineal (elastoplástica o rigidoplástica). Otro caso típico en estructura metálica lo constituyen los tirantes, que no soportan compresiones y que en tracción pueden alcanzar un límite de cedencia o plastificación-ver ejemplo 3. En el caso de estructuras de hormigón armado, el problema está en la pérdida progresiva de rigidez a flexión al irse fisurando la sección, y en que el hormigón armado posee una gráfica tensión – deformación no lineal. También es el caso de coacciones exteriores -apoyos o empotramientos- no lineales, tales como las losas de cimentación donde los desplazamientos hacia abajo producen reacciones que crecen linealmente, pero en el sentido contrario se produce un ‘despegue’ cimiento – terreno y por tanto sin coacción ni reacción, y por último, los apoyos simples unidireccionales en los que en un sentido hay apoyo y por tanto reacción, y en el otro no hay coacción ni por tanto reacción (ver ejemplo 4).
El cálculo en 2º orden geométrico es más sencillo de abordar y requiere un menor coste en tiempo de cálculo que el cálculo en 2º orden mecánico. Normalmente, o bien se aborda un cálculo en 2º orden geométrico, o bien se abordan ambos tipos en un mismo proceso.
Tricalc permite considerar el cálculo en 2º orden geométrico o elástico, así como el cálculo en 2º orden mecánico o plástico, en el caso de tirantes, de apoyos unidireccionales y de resortes unidireccionales en losas de cimentación (versión 7.2)
Criterios de convergencia
En el cálculo en 2º orden, al utilizarse un proceso iterativo de aproximaciones sucesivas, hay que establecer un criterio que indique cuándo se ha llegado a la solución deseada. En general, se adopta un doble criterio: que los desplazamientos o esfuerzos calculados en una iteración sean suficientemente próximos a los de la iteración anterior, y que no se supere un determinado número de iteraciones. Por ejemplo, en Tricalc, el usuario puede fijar la diferencia máxima en desplazamiento entre dos iteraciones de todos los nudos de la estructura.
Resolución en 2º orden geométrico o elástico
Para resolver el cálculo de esfuerzos en 2º orden geométrico o elástico, es necesario resolver el sistema de ecuaciones
([K] – [GN]) ·{d} = {F}
Que también puede escribirse como
[K]·{d} = {F} – [GN]·{d}
La matriz [GN] es la matriz geométrica de rigidez y define la relación entre [K] ó {F] con los desplazamientos de la iteración anterior. Por tanto, puede resolverse de dos maneras: calculando en cada iteración la matriz ([K] – [GN]), o bien, modificando en cada iteración el vector de acciones exteriores {F} – [GN]·{d}. Tricalc ha optado por ejemplo, por el segundo método, en el que la matriz de rigidez permanece constante en todas las iteraciones y combinaciones de acciones.
Este tipo de cálculo tiene la particularidad de que la relación entre deformación y acciones adicionales de 2º orden es constante (Hi = P·D i / h, como vimos en el ejemplo), lo que implica que no es necesario tener en cuenta la historia de carga de la estructura.
Resolución del cálculo en 2º orden mecánico o plástico
En este caso, tras cada iteración es necesario modificar la matriz de rigidez [K]. Dependiendo del fenómeno de 2º orden estudiado, la modificación será más o menos compleja y requerirá más o menos tiempo de cálculo.
En el caso de tirantes, en los que sólo se desea evitar que trabajen a compresión, basta tras cada iteración, eliminar de la matriz de rigidez los tirantes que trabajan a compresión, teniendo en cuenta que si en una iteración un tirante estaba comprimido, en la iteración siguiente puede estar traccionado y viceversa. Además, al igual que en el caso de cálculo de 2º orden geométrico, tampoco es necesario considerar la historia de carga de la estructura.
En el caso de formación de rótulas plásticas o de que se produzca la plastificación del material, al producirse una deformación irreversible, sí es necesario considerar la historia de carga. Es decir, para estudiar una combinación de acciones, es necesario dividir el tiempo en diferentes estados de carga intermedios y partir en cada estado de las deformaciones irreversibles producidas en el estado anterior. Lo mismo ocurre con fenómenos derivados de la fisuración en hormigón armado: una vez que una sección ha fisurado (y por tanto su rigidez ha disminuido a veces drásticamente) no vuelve a su estado anterior aunque disminuyan las cargas. En el caso del hormigón armado existe la dificultad adicional de que la rigidez fisurada depende de la armadura de la pieza, que en general no se conoce antes de abordar el cálculo, lo que implica un primer cálculo para estimar la armadura y, si tras una iteración fuera necesario modificar la armadura sustancialmente, se debería reiniciar todo el proceso de cálculo. Hay que decir no obstante, que hay normas como el Eurocódigo 2 (EN 1992-1-1:2004) en las que de forma simplificada, puede adoptarse una rigidez reducida que ya no depende de la armadura ni de la historia de carga, transformándose el problema en uno de 1º orden.
Cuando interviene la historia de carga, es necesario además adoptar técnicas de cálculo más refinadas como pasar de un estado de carga al siguiente mediante pequeños incrementos de carga. Además, en fase de proyecto, no siempre es conocido el proceso constructivo que tendrá la estructura y por tanto, es difícilmente predecible la historia de carga.
Como ya se ha indicado, Tricalc permite opcionalmente la consideración de los tirantes (ver ejemplo 3) y apoyos unidireccionales (ver ejemplo 4), definidos en cualquier parte de la estructura con absoluta libertad. En el caso de habilitarse esta consideración y de que existan barras consideradas como tirantes en la estructura, Tricalc modifica la matriz de rigidez tras cada iteración (de cada combinación de esfuerzos estudiada en 2º orden) para eliminar de ella los tirantes que resultaran comprimidos en la iteración anterior.
Estructuras calculables en 2º orden
A continuación se muestran algunos ejemplos de estructuras claramente traslacionales, en las que es necesario considerar los esfuerzos adicionales que se producen al aplicar las fuerzas exteriores en su posición de deformada.
En el ejemplo 1, la aplicación de la carga puntual en el extremo del voladizo produce unos efectos de 2º orden a considerar, que incrementan los esfuerzos en el pilar.

Ejemplo 1, Estructura traslacional
En el ejemplo 2, la estructura tiene una carga superior importante. Cualquier variación en la posición de la carga incrementa los esfuerzos del pilar por la aplicación de la carga en la posición deformada.
 |
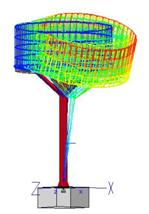 |
Ejemplo 2, Estructura con importante carga
superior, que condiciona el dimensionado del pilar
al considerar la hipótesis de desplazamientos de la carga.
En el ejemplo 3, el testero de una nave, se han dispuesto unos tirantes contra la acción del viento lateral que sólo deben trabajar a tracción, lo que condiciona también los esfuerzos y desplazamientos del resto de los elementos. Obsérvese que los tirantes no tienen por qué formar cruces de San Andrés ni estar dispuestos en la diagonal de un rectángulo.
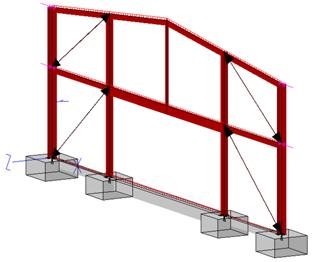
Ejemplo 3, Estructura con tirantes para la est abilidad lateral, que sólodeben trabajar a tracción.
En el ejemplo 4, vemos el caso de una viga de tres vanos apoyada en la coronación de sendos muros de fábrica. Estos apoyos impiden el descenso de la viga, pero no así su levantamiento. La alternancia de sobrecargas hace que cuando sólo el vano central está cargado, la viga se ‘despegue’ de los apoyos extremos. Para su cálculo, los apoyos se han modelizado mediante pilares superiores de gran rigidez pero con la condición de tirante.
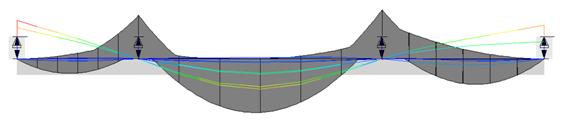

Ejemplo 4, Estructura con apoyos unidireccionales modelizados con tirantes. En la imagen superior, calculada en 2º orden, en el que se observa el ‘despegue’ de los apoyos extremos en algunas combinaciones. En la imagen inferior, resultados del
1º orden, donde no es posible tener en cuenta este tipo de apoyo (en los apoyos extremos se producen reacciones hacia abajo en algunas combinaciones).Tiempos de cálculo
Es difícil determinar el tiempo de cálculo adicional que supone un cálculo de esfuerzos en 2º orden, sobre todo porque va a depender de la velocidad de convergencia hacia la solución. Como ejemplo, para una estructura de una nave industrial metálica con cubierta tipo dientes de sierra, calculada con viento y sismo, tiene 1.277 barras, 622 nudos y 3.456 grados de libertad, se tiene:
| Tipo de cálculo | Cálculo Esfuerzos y Desplazamientos | Cálculo incluyendo dimensionado |
| 1º Orden | 14" | 4’13" |
|
2º Orden sin tirantes |
6’ 7" ( 1042 iteraciones. 1,2" por iteración) |
17’ 22" |
| 2º Orden con tirantes |
7’ 49" (1230 iteraciones. 1,6" por iteración) |
19’ 13" |
Criterio de convergencia utilizado en 2º Orden, igual a 0,001cm
de diferencia entre los desplazamiento de 2 iteraciones sucesivas.
275 combinaciones calculadas en 2º orden.
Beneficios del método de cálculo utilizado por Tricalc
Si un cálculo en 2º orden produce siempre mayores desplazamientos y por tanto, mayores esfuerzos, cabe preguntarse por qué realizar un cálculo en 2º orden si hay otros métodos que igualmente permite la normativa.
En el caso de los tirantes (elementos que sólo resisten tracciones) la respuesta es evidente: el cálculo en 2º orden es el único que puede tener en cuenta de una manera precisa y general este tipo de elementos. Aunque haya métodos aproximados para tenerlos en cuenta sin necesidad de acudir a un cálculo en 2º orden, no dejan de ser simplificaciones que exigen tales condicionamientos geométricos que restringen en gran medida su aplicabilidad.
En el caso de los apoyos unidireccionales, es posible eliminar en cada iteración los elementos que no trabajan como han sido definidos. Por ejemplo, en los apoyos unidireccionales, en el caso que en una determinada combinación trabajen a compresión, pueden ser eliminados en la siguiente iteración dejando sólo los que estén traccionados.
También se produce un gran beneficio en el correcto cálculo de estructuras esbeltas o ‘traslacionales’, incluso posibilitando el uso de secciones menores respecto a otros métodos más simplificados de considerar el estado límite último de inestabilidad o pandeo.
Efectivamente, a falta de un estudio más profundo (objeto tal vez de otro artículo), la consideración del estado límite último de inestabilidad o pandeo de un pilar para estructuras traslacionales o de nudos desplazables definido en las diferentes normativas de hormigón, acero y madera, se puede realizar mediante los tres métodos siguientes:
| Tipo de cálculo | Comprobación a pandeo-longitud de pandeo |
| A) 1º Orden | Elemento Traslacional,, Lp = b·L, con b Î [1; ¥] |
| B) 1º Orden con coeficientes de amplificación | Elemento Intraslacional,, Lp = b·L, con b Î [0,5; 1] |
| C) 2º Orden | No necesaria |
Se entiende siempre para estructuras traslacionales
El método A es el más inexacto y el más antiguo. Está sujeto además a muchas incertidumbres, ya que es muy sensible a la correcta selección del parámetro b que tiene un rango de valores posibles demasiado elevado.
El método B es más preciso en cuanto que la variabilidad de b es muy reducida. Sin embargo, es sensible a la correcta elección de los denominados coeficientes de amplificación, que en algunos casos (estructuras que no son forjados horizontales con pilares verticales como el caso de naves industriales, o pandeo de elementos comprimidos no verticales) no son fáciles de obtener.
El método C es el que muchas normas denominan ‘caso general’. Es el más preciso de todos, pero en algunos casos (sobre todo en hormigón armado o cuando hay que comprobar el pandeo lateral o torsional) es de muy difícil implementación.
El cálculo en 2º orden realizado por Tricalc se sitúa en los métodos B y C: Se calcula la longitud de pandeo como elemento intraslacional ( Lp = b·L, con b Î [0,5; 1]) y se comprueba el pandeo con métodos del tipo ‘columna modelo’. Sólo en algunos casos (elementos metálicos no sensibles al pandeo lateral o torsional, como secciones huecas o en cajón) podría utilizarse en Tricalc el método C (es decir, cálculo en 2º orden geométrico o elástico considerando las imperfecciones globales y locales y no comprobar a pandeo).
Por tanto, el cálculo en 2º orden de Tricalc tiene las siguientes ventajas respecto a los métodos A y B:
Conclusión
© Arktec, S.A. 2009